1 引言
B+树是在B树基础进一步优化得到的一种数据结构。B+树相比于B树具有更高的查询效率。
2 定义
B+树定义:
(1)B+树包含2种类型的结点:内部结点(也称索引结点)和叶子结点。
(2)根结点本身即可以是内部结点,也可以是叶子结点。根结点的关键字个数最少可以只有1个。
(3)B+树与B树最大的不同是内部结点不保存数据,只用于索引,所有数据(或者说记录)都保存在叶子结点中。
(4) m阶B+树表示了内部结点最多有m-1个关键字(或者说内部结点最多有m个子树),阶数m同时限制了叶子结点最多存储m-1个数据。
(5)内部结点中的key都按照从小到大的顺序排列,对于内部结点中的一个key,左树中的所有key都小于它,右子树中的key都大于等于它。叶子结点中的数据也按照key的大小排列。
(6)每个叶子结点都存有相邻叶子结点的指针,叶子结点本身依关键字的大小自小而大顺序链接。
B+树示意图:
图2.1所示的B+树中,灰色节点代表索引节点,索引节点中只有key,而不含数据data。橙色节点代表叶子节点,叶子节点中既有key值又有数据data。叶子节点采用单链表的方式链接。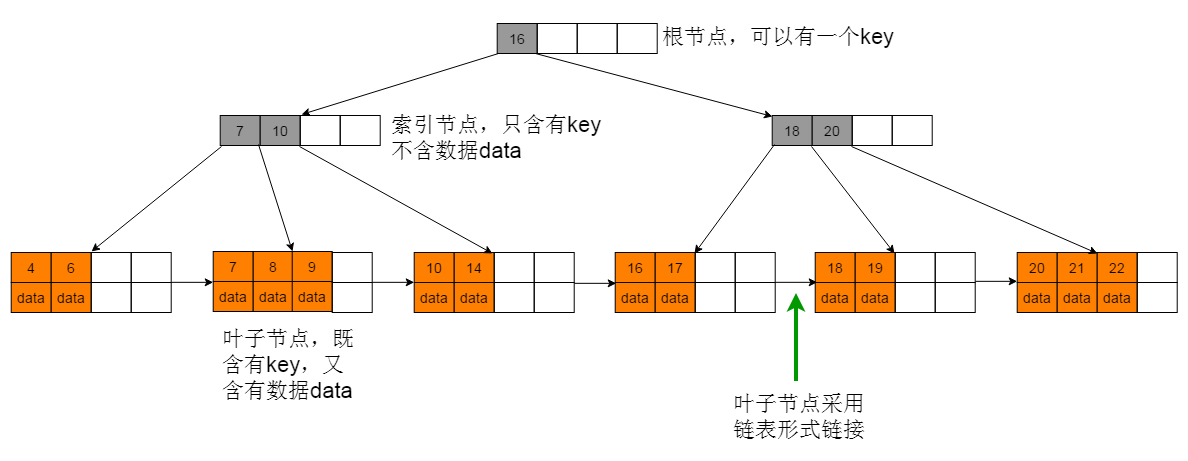
图2.1 B+树
3 特点
(1)索引节点的key值均会出现在叶子节点中。
(2)索引节点中的key值在叶子节点中或者为最大值或者为最小值。
(3)叶子节点使用单链表的形式链接起来。
4 插入
4.1 插入流程
B+树的插入流程与B树类似,对于m阶的B+树,插入数据情况如下:
(1) 若当前树为空树,则创建一个叶子结点,然后将记录插入其中,此时这个叶子结点也是根结点,插入操作结束。
(2)针对叶子类型结点:根据key值找到叶子结点,向这个叶子结点插入数据。插入后分两种情形:
(2)- A:插入后,若当前结点中包含key的个数小于或者等于m-1,则插入结束。
(2)- B:插入后,当前结点key的个数大于m-1,将这个叶子结点分裂成左右两个叶子结点,左叶子结点包含前m/2个数据,右结点包含剩下的数据,将第m/2+1个记录的key进位到父结点中(父结点一定是索引类型结点),进位到父结点的key左孩子指针向左结点,右孩子指针向右结点。将当前结点的指针指向父结点,然后执行第(3)步。
(3)针对索引类型结点,同样分为两种情形:
(3)- A:若当前结点key的个数小于等于m-1,则插入结束。
(3)- B:若当前节点key的个数大于m-1,将这个索引类型结点分裂成两个索引结点,左索引结点包含前(m-1)/2个key,右结点包含m-(m-1)/2个key,将第m/2个key进位到父结点中,进位到父结点的key左孩子指向左结点, 进位到父结点的key右孩子指向右结点。将当前结点的指针指向父结点,然后重复第(3)步。
4.2 实例图解
以5阶B+树为例,介绍B+树的数据插入过程。
图解过程:
1:首先,插入4,符合情形(1),将插入数据4作为根节点。
2:继续插入8,10,14,符合情形(2)- A。直接插入数据到根节点。
3:插入16,当前节点中key数目超过4,符合情形(2)- B,因此需要进行节点分裂。分裂后增加索引节点,插入索引节点符合情形(3)- A。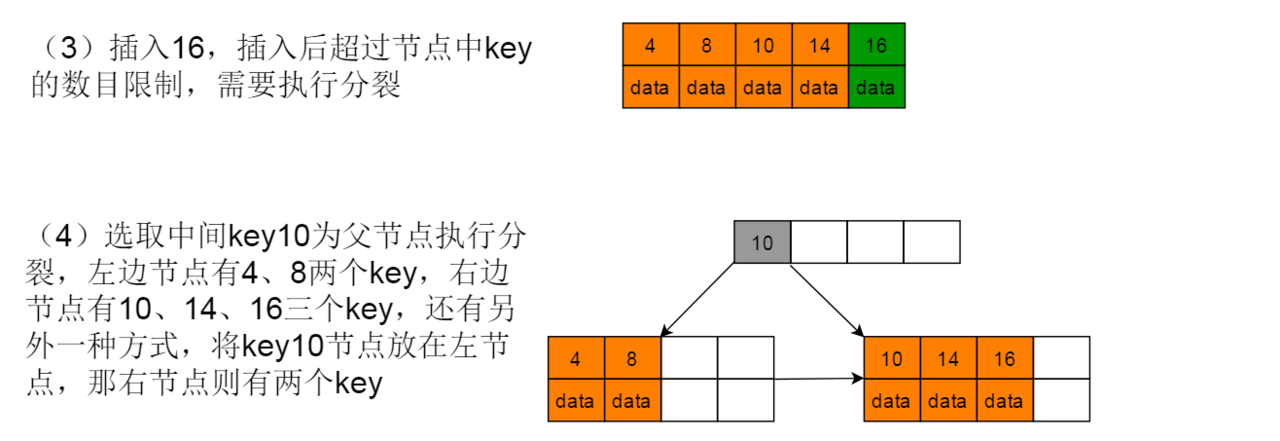
4:继续插入17,18,插入18后,符合情形2-b,节点16作为索引节点完成插入,符合情形(3)- A。将中间key值16作为索引节点上移至父节点中。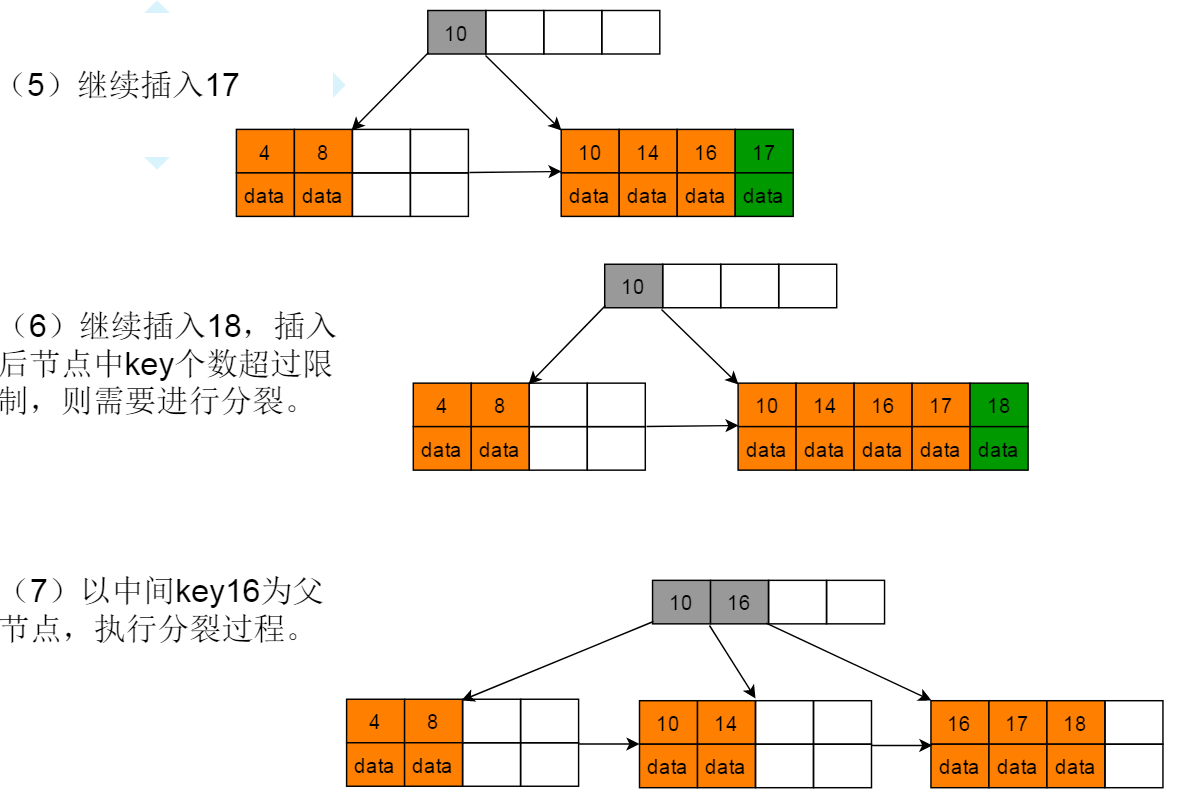
5:按照相同步骤继续插入6,9,19,20,21,22。
6:继续插入7,符合情形(2)- B,节点7作为索引节点插入时,符合情形(3)- B,进行索引节点分裂。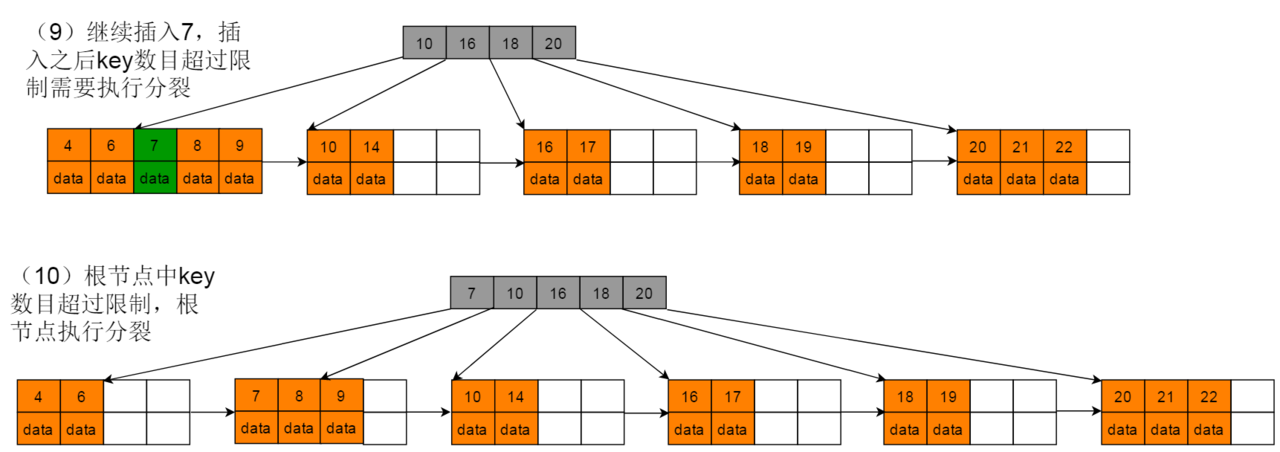
7:索引节点分裂完毕,插入过程结束。
5 删除
5.1 删除流程
B+树在进行数据的删除之前,需要执行数据key的查找过程。B+树的查找结束位置一定是在叶子节点。如果叶子结点中没有相应的key,则删除失败。否则执行下面的步骤进行数据删除:
(1)删除叶子结点中对应的key。删除后若结点的key的个数大于等于Math.ceil(m-1)/2 – 1,删除操作结束,否则执行第(2)步。
(2)若兄弟结点key数目大于Math.ceil(m-1)/2 – 1,向兄弟结点借一个数据,同时用借到的key替换父结(指当前结点和兄弟结点共同的父结点)点中的key,删除结束。否则执行第(3)步。
(3)若兄弟结点中key数目小于Math.ceil(m-1)/2 – 1,则当前结点和兄弟结点合并成一个新的叶子结点,并删除父结点中的key(父结点中的这个key两边的孩子指针就变成了一个指针,正好指向这个新的叶子结点),将当前结点指向父结点(必为索引结点),执行第(4)步。
(4)若索引结点的key的个数大于等于Math.ceil(m-1)/2 – 1,则删除操作结束。否则执行第(5)步
(5)若当前节点的兄弟结点key数目大于等于Math.ceil(m-1)/2 – 1,父结点key下移,兄弟结点key上移,删除结束。否则执行第(6)步
(6)当前结点和兄弟结点及父结点下移key合并成一个新的结点。将当前结点指向父结点,重复第(4)步。
注意,通过B+树的删除操作后,索引结点中存在的key,不一定在叶子结点中存在对应的记录。
5.2 实例图解
以4.2节中的5阶B+树为例,逐步说明B+树的删除过程。
图解过程
1:首先,删除数据22,符合情形(1),直接删除22数据即可。*
2:删除22后,继续删除数据14。删除14后,当前节点只有一个key,兄弟节点有三个key,符合情形(2)。当前节点只有一个key10,,兄弟节点有3个key,向兄弟节点借一个key为9的数据,并将父节点中的key10变为key9。


3:删除14后,继续删除数据7。删除数据7后,符合情形(3)。当前节点只有一个key8,且兄弟节点只有两个key,将当前节点与兄弟节点进行合并。

4:合并完后当前节点只含有一个key,兄弟节点只有两个key,继续合并。
5:合并完成,删除过程结束,树的高度降低。
6 结语
在实际的数据库索引以及文件存储都是使用B+树实现的,那么,B+树相比于B树有哪些优点呢?
(1)B+树中索引节点只存储key值,不存储数据,则相同的大小磁盘页中,使用B+树可以存储更多的节点元素,使得B+树比B树更为矮胖,减少磁盘IO次数。
(2)在查找单一元素时,B树最好情况是在根节点查找成功,最坏情况是查找至叶子节点,导致B树的查找过程是不稳定的。而使用B+—树的查找最终查找节点为叶子节点,使得B+树查找稳定。
(3)在进行某个范围内数据查找,B树需要进行中序遍历,而B+树的叶子节点采用单链表形式链接,只需按顺序遍历链表即可完成范围查找,提高了查找效率。