数据结构与算法--霍夫曼树

Posted on

1 概述

  霍夫曼编码是一种基于最小冗余编码的压缩算法。最小冗余编码是指，如果知道一组数据中符号出现的频率，就可以用一种特殊的方式来表示符号从而减少数据需要的存储空间。霍夫曼编码过程如下：

2 统计字符频率

  例如：有如下字符串：
  A A C B C A A D D B B A D D A A B B

得到各个字符频率如下表：

字符 频率
A 7
B 5
C 2
D 4

3 构造霍夫曼树

3.1 霍夫曼树定义

  霍夫曼树：给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。结合第2节中的字符串，将字符串出现频率作为权值。

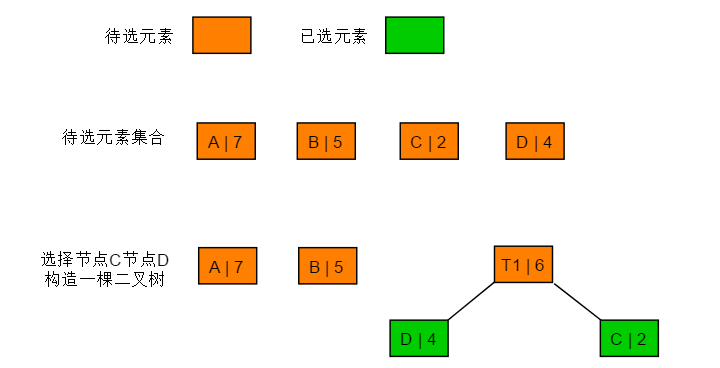
3.2 构造流程

（1）选取权值最小和次小的节点作为左右子树，构造一棵二叉树。
（2）将步骤1构造的二叉树的根节点的权值设置为，左右子树之和。
（3）去除步骤1中已经选过的节点，将新的二叉树的根节点加入至待选集合
（4）继续重复步骤1，直至仅剩一个元素未选中。

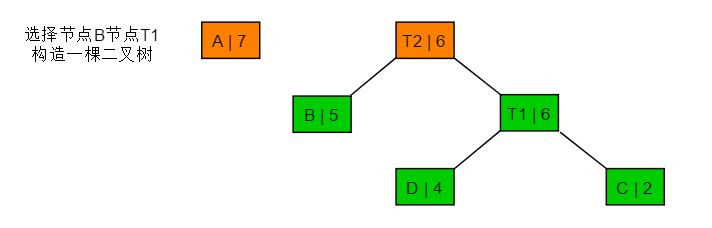
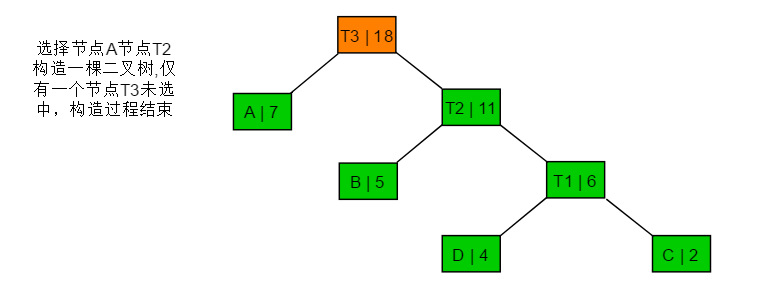
3.3 图解过程

img

img

img

  通过构造的霍夫曼树可以看出，权值越大的节点距离根节点越近，其深度越小，权值越小的节点，距离根节点越远，其深度越大。

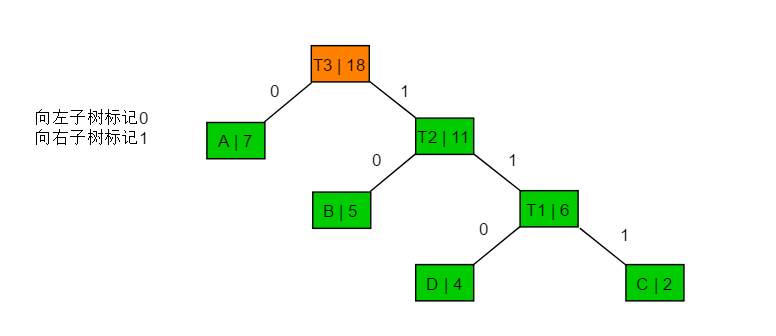
4 霍夫曼编码

  在经过步骤3，构造出霍夫曼树后，对霍夫曼树执行遍历。将向左子树路径标记为0，向右子树的路径标记为1。则标记后的霍夫曼树为：

图4.1

图4.1

  按照图4.1进行霍夫曼编码为：

数据 编码
A 0
B 10
C 111
D 110

  A A C B C A A D D B B A D D A A B B 编码后的数据长度为：
  0 0 111 10 111 0 0 110 110 10 10 0 110 110 0 0 10 10 编码长度为35。

  若采用等长编码为：

数据 编码
A 00
B 01
C 10
D 11

  则A A C B C A A D D B B A D D A A B B对应编码为：
  00 00 10 01 10 00 00 11 11 01 01 00 11 11 00 00 01 01
  编码长度为36。可以看出使用霍夫曼编码可以缩短数据编码长度，达到数据压缩的效果。当字符数目较少时不能体现霍夫曼编码带来的压缩效果，但是当字符数目较多时，霍夫曼编码的压缩效率将显著提高。

5 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
#include<iostream>  
#include<string>  
using namespace std;

struct Node
{
    double weight;  //存储权值
    string ch;  //存储字符
    string code; //编码
    int lchild, rchild, parent;//分别存储左孩子、右孩子、父节点位置
};

void Select(Node huffTree[], int *a, int *b, int n)//找权值最小的两个a和b  
{
    int i;
    double weight = 0; //找最小的数
    for (i = 0; i <n; i++)
    {
        if (huffTree[i].parent != -1)     //判断节点是否已经选过
            continue;
        else
        {
            if (weight == 0)
            {
                weight = huffTree[i].weight;
                *a = i;
            }
            else
            {
                if (huffTree[i].weight < weight)
                {
                    weight = huffTree[i].weight;
                    *a = i;
                }
            }
        }
    }
    weight = 0; //找第二小的数
    for (i = 0; i < n; i++)
    {
        if (huffTree[i].parent != -1 || (i == *a))//排除已选过的数
            continue;
        else
        {
            if (weight == 0)
            {
                weight = huffTree[i].weight;
                *b = i;
            }
            else
            {
                if (huffTree[i].weight  < weight)
                {
                    weight = huffTree[i].weight;
                    *b = i;
                }
            }
        }
    }
    int temp;
    if (huffTree[*a].lchild < huffTree[*b].lchild)  //小的数放左边
    {
        temp = *a;
        *a = *b;
        *b = temp;
    }
}

void Huff_Tree(Node huffTree[], int w[], string ch[], int n)
{
    for (int i = 0; i < 2 * n - 1; i++) //初始过程
    {
        huffTree[i].parent = -1;    
        huffTree[i].lchild = -1;    
        huffTree[i].rchild = -1;  
        huffTree[i].code = "";
    }
    for (int i = 0; i < n; i++)       
    {
        huffTree[i].weight = w[i];  
        huffTree[i].ch = ch[i];     
    }
    for (int k = n; k < 2 * n - 1; k++)
    {
        int i1 = 0;
        int i2 = 0;
        Select(huffTree, &i1, &i2, k); //将i1，i2节点合成节点k
        huffTree[i1].parent = k;   
        huffTree[i2].parent = k;
        huffTree[k].weight = huffTree[i1].weight + huffTree[i2].weight;
        huffTree[k].lchild = i1;
        huffTree[k].rchild = i2;
    }
}

void Huff_Code(Node huffTree[], int n)
{
    int i, j, k;
    string s = "";
    for (i = 0; i < n; i++)  
    {
        s = "";         
        j = i;                
        while (huffTree[j].parent != -1) //从叶子往上找到根节点
        {
            k = huffTree[j].parent;
            if (j == huffTree[k].lchild) //如果是根的左孩子，则记为0
            {
                s = s + "0";
            }
            else               
            {
                s = s + "1";
            }
            j = huffTree[j].parent; 
        }
        cout << "字符 " << huffTree[i].ch << " 的编码：";
        for (int l = s.size() - 1; l >= 0; l--)    
        {
            cout << s[l];
            huffTree[i].code += s[l]; //保存编码
        }
        cout << endl;
    }
}

string Huff_Decode(Node huffTree[], int n,string s)
{
    cout << "解码后为：";
    string temp = "",str="";//保存解码后的字符串
    for (int i = 0; i < s.size(); i++)
    {
        temp = temp + s[i];
        for (int j = 0; j < n; j++)
        {    
            if (temp == huffTree[j].code)
            {
                str=str+ huffTree[j].ch;
                temp = "";
                break;
            }    
            else if (i == s.size()-1&&j==n-1&&temp!="")//全部遍历后没有
            {
                str= "解码错误！";
            }
        }
    }
    return str;
}
Rick Smith